와이코프 이론 패턴

AndyVentura • 2025. 4. 28. 오후 8:11:11

와이코프 이론 패턴**은 금융시장에서 시장 행동과 가격 움직임을 이해하기 위한 오랜 기간 검증된 접근법입니다. 20세기 초 리차드 와이코프(Richard D. Wyckoff)가 개발한 이 이론은 트레이더와 투자자에게 가격 움직임과 시장 추세를 분석할 수 있는 프레임워크를 제공합니다. 특히 기술적 분석과 트레이딩 분야에서 잘 알려져 있으며 공급, 수요, 축적, 유통의 역학에 대한 귀중한 통찰력을 제공합니다.

와이코프 이론의 핵심 원리 ### 와이코프 이론의 핵심 원리

와이코프 이론은 시장이 은행과 대형 헤지펀드 등 기관 투자자의 행동에 영향을 받는다는 생각에 기반한 이론으로, “복합 운영자”라고도 합니다. 와이코프는 가격 차트와 거래량 패턴을 연구하면 개인 트레이더가 대형 트레이더와 맞서 거래하는 것이 아니라 이들의 의도에 맞춰 전략을 조정할 수 있다고 강조했습니다.

와이코프 이론의 핵심 원칙 중 하나는 축적, 마크업, 분배, 마크다운 등 ‘가격 사이클’에 대한 이해입니다. 이러한 단계는 수요와 공급의 불균형에 따라 가격이 움직이는 반복적인 과정을 설명합니다.

축적 단계: 축적 단계에서는 대형 기관 투자자들이 하락 추세 이후 낮은 가격에 조용히 자산을 매수하기 시작합니다. 이 단계는 가격이 크게 상승하지 않고 스마트 머니가 포지션을 축적하면서 가격이 일정 범위 내에서 거래되는 통합이 특징입니다.
마크업 단계: 축적이 완료되면 상승 추세가 시작됩니다. 이 단계에서는 더 많은 트레이더가 랠리에 참여하면서 가격이 상승하는데, 스마트 머니가 훨씬 일찍 추세를 시작했다는 사실을 인지하지 못하는 경우가 많습니다.
분배 단계: 유통 단계에서는 기관 투자자가 보유 자산을 경험이 적은 개인 트레이더에게 높은 가격에 매도하기 시작합니다. 스마트 머니가 시장에서 빠져나가면서 가격은 다시 통합되어 상승 추세가 약화됩니다.
마크다운 단계: 매도세가 매수세보다 많아지면서 가격이 하락하고 사이클이 새롭게 시작되는 하락 단계가 이어집니다.

와이코프 가격 사이클 ### 와이코프 가격 사이클

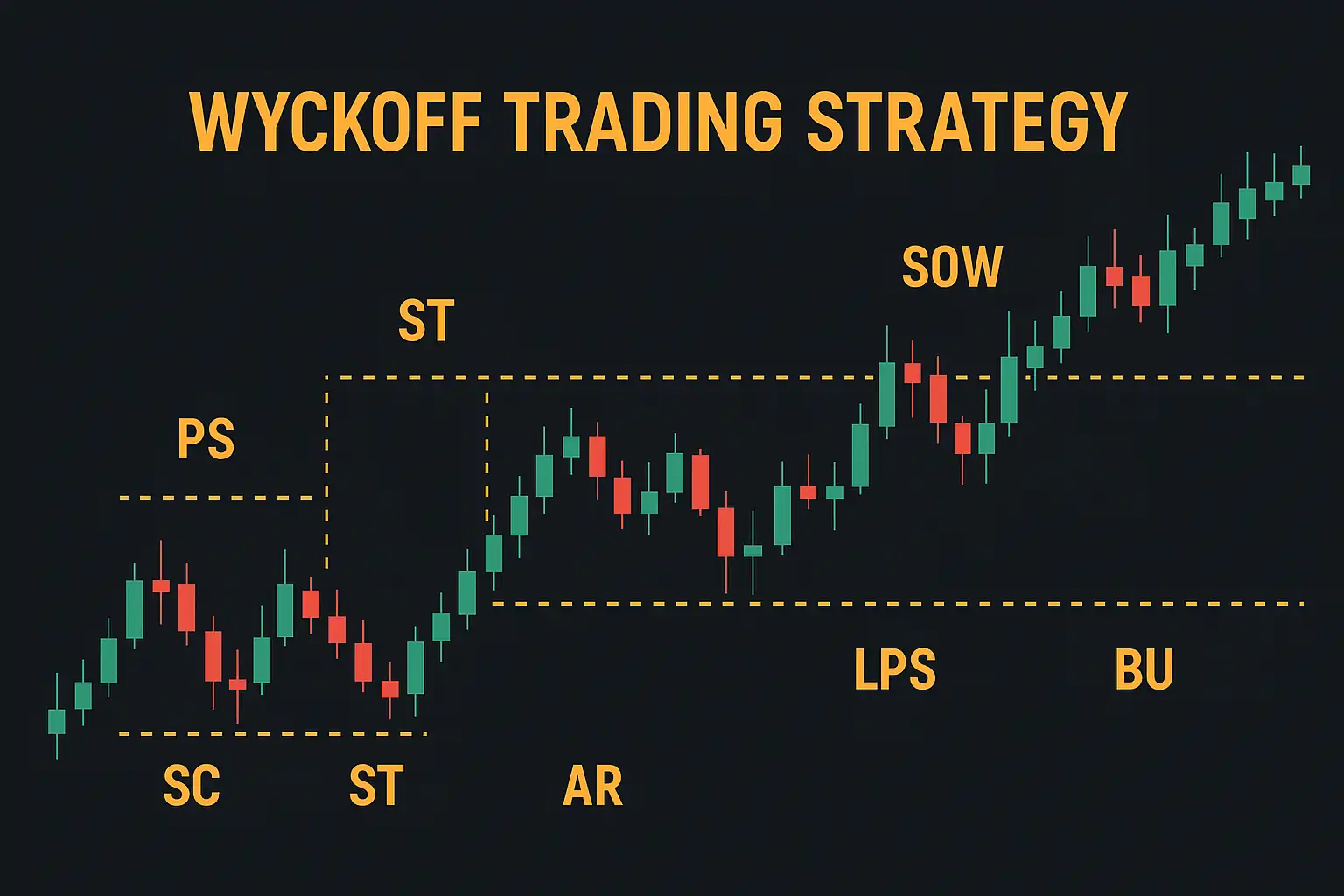
와이코프의 가격 주기에는 트레이더가 향후 시장 움직임을 예측하는 데 사용하는 주요 패턴과 구조가 포함되어 있습니다. 가장 잘 알려진 패턴 중 하나는 축적 및 분배 단계의 가격 움직임을 설명하는 와이코프 도식입니다. 이 도식에는 예비 지지(PS), 매도 클라이맥스(SC), 자동 랠리(AR), 스프링 등 다양한 단계가 포함됩니다.

누적 도식**: 이 패턴은 종합 트레이더가 자산을 축적하는 기간을 반영합니다. 약세 수급이 시장에서 빠져나가면서 가격이 박스권 내에서 유지되어 스마트 머니가 진입할 수 있는 기회가 생깁니다. “봄” 단계는 가격이 지지선 아래로 하락하여 손절매가 발생하고 기관 트레이더에게 마크업 단계가 시작되기 전에 낮은 수준에서 추가 매수할 기회를 제공할 때 발생합니다.
분배 도식**: 반대로 유통 구간에서는 스마트 머니가 보유 자산을 매도하면서 가격이 횡보합니다. 이와 유사한 이벤트인 “업스트러스트”는 저항선을 돌파하는 잘못된 신호로, 인하 단계가 시작되기 전에 경험이 없는 매수자를 가두는 역할을 합니다.

와이코프 법칙과 트레이딩 원칙

와이코프는 트레이더를 안내하기 위해 세 가지 기본 법칙을 정립했습니다:

수요와 공급의 법칙: 가격 변동은 수요와 공급의 상대적 균형에 따라 달라집니다. 수요가 공급을 초과하면 가격이 상승하고 공급이 수요를 초과하면 가격이 하락합니다.
노력 대 결과의 법칙: 움직임의 강도를 확인하려면 거래량이 가격 움직임과 일치해야 합니다. 거래량이 충분하지 않은 상태에서 큰 가격 변동이 발생하면 잠재적인 반전의 신호일 수 있습니다.
원인과 결과의 법칙: 누적 또는 분포는 향후 추세를 결정하는 “원인” 또는 “결과”를 만듭니다. 누적 또는 분포 범위가 클수록 결과 추세가 더 강해집니다.

결론

와이코프 이론 패턴은 현대 금융 시장에서 가격 움직임 분석의 초석으로 남아 있습니다. 축적, 마크업, 분배, 마크다운의 기본 역학을 이해함으로써 트레이더는 시장 추세를 더 잘 예측하고 스마트 머니에 맞춰 전략을 조정할 수 있습니다. 인내심과 연습이 필요하지만 와이코프 이론은 트레이더에게 시장 움직임의 복잡성을 헤쳐나갈 수 있는 강력한 방법론을 제공합니다.